Лук, работа, энергия, КПД. Приглашение к дискуссии, так сказать.

[Morceleb]

Собственно говоря, тут будет много банальностей, которые должны быть известны каждому еще со школьной скамьи, однако многие подзабыли, в том числе и я, поэтому освежаю память.
Первая предпосылка - рассматривать максимально упрощенную модель.
1. Плечи лука, пожалуй, стоит рассматривать как плоские пружины изгиба.
2. Для определения потенциальной энергии лука можно использовать формулу: E=((Fm+F1)/2)*L*КПД
где: Fm - сила на тетиве при максимальном растяжении
F1 - сила на тетиве в начальной точке (никогда не будет нулевой даже для простого лука, а уж тем более для рекурсивного). Как ни странно, во многих математических моделях, исследующих работу лука, с виду довольно серьезных, ее игнороруют, а очень зря. Лук в снаряженном состоянии - это уже напряженная балка.
L-ход тетивы
Поясню почему - поскольку здесь не ставится задача глубокого исследования, а все формулы будут для примерного определения параметров лука с точностью 0 целых хер десятых, пущай изменение силы натяжения по ходу тетивы будет линейным. На самом деле это не совсем так, силовая характеристика лука нелинейна, но углубляться в теорию упругости нет ни желания, ни (как ни странно) необходимости. В любом случае, это все придет к интегралу силы по перемещению и в пределе выродится в определение площади трапеции (что мы и видим).
КПД- коэффициент полезного действия, зависящий от массы и материала плеч лука, массы и материала тетивы, веса стрелы etc. Для луков разных конструкций колеблется от 25 до 70%(70% - это для блочных луков с оптимально подобранным весом стрелы, изготовленных из современных материалов и так далее).
Если известна масса стрелы и ее начальная скорость, определить КПД проще простого - кинетическую энергию стрелы делим на потенциальную энергию и вуаля. Нужно только учесть, что при изменении массы стрелы будет меняться и КПД лука. То есть подход "определим кпд лука со стрелой весом в 50 г и исходя из этого посчитаем начальную скорость для стрелы весом в 25 г" не работает. Увы.
Казалось бы, чем легче стрела, тем быстрее и дальше она полетит, ан нет.
Начнем с того, что при выстреле из лука энергия тратится кроме разгона стрелы на разгон движущихся частей лука, часть энергии теряется, выделяясь в виде нагрева конструкции и т.д. Поэтому теоретическая скорость максимально облегченной стрелы ограничена (в пределе) максимальной скоростью тетивы при холостом выстреле. Для тяжелой стрелы тоже есть предел - слишком тяжелая стрела увеличивает отдачу лука, что заметно снижает точность. В прошлом, сдается мне, подбор идеального веса стрелы шел эмпирически.

Зависимость КПД лука от веса стрелы (тырено из криминалистического исследования).
Отсюда же становится совершенно понятной зависимость, отмеченная Поупом - лук с легкими упругими плечами стреляет дальше и лучше, чем тяжелый. Тут теория и практика совпадают совершенно точно - чем тяжелее плечи при том же усилии натяжения, тем ниже КПД лука. Фактически, при одном и том же усилии натяжения, луки изготовленные из разных материалов могут иметь энергию выстрела различающуюся чуть ли не вдвое. Большой наш привет художникам, которые рисуею супер-пупер луки для игр - чем больше херни прикручено на плечи лука, тем хуже он будет стрелять.

Пример лука для ближнего боя. Далеко все равно не выстрелит
И вот тут мы приходим к еще одному парадоксу, связанному с луками: мощность лука, определяемая как отношение запасенной энергии ко времени выстрела (разгибания плеч) максимальна при.... минимальной массе стрелы, а еще лучше при холостом выстреле. Чем тяжелее стрела - тем ниже мощность. Соответственно, для получения максимальной мощности стрелу нужно облегчать, но для наиболее полного перехода потенциальной энергии в кинетическую ее нужно утяжелять.
Как обычно, ищем компромисс.
Прикидываем потенциальную энергию для лонгбоу с максимальным усилием натяжения 70 фунтов. На начальном участке сила натяжения не превышает 10 фунтов по словам стрелков из этого самого лонгбоу. Собственный КПД лука примем равным 30% (довольно примитивная конструкция, не самые лучшие материалы).
E=((Fm+F1)/2)*L*КПД=(315+45)/2*0.6*0.3=129.3.
Порядка 129 джоулей.
Теоретически энергия стрелы при оптимальном ее подборе - 129х0.85=110 дж.

Для проверки берем стрелу весом в 50 г. Теоретически ее скорость составит 66 м/с что весьма похоже на правду.

Увеличиваем массу вдвое (тяжелая стрела) - теоретический КПД падает до 80%, энергия, соответственно, падает до 129х0.8=103дж, скорость до 45 м/с, что, кстати, совпадает с экспериментальными данными, если верить тому же Поупу.

Уменьшаем массу стрелы до 25 г (теоретический КПД - 65%)

Энергия выстрела: 129х0.65=84 дж
Скорость стрелы - 82 м/с, что тоже довольно близко к практическим результатам.
Данные по 60-ти фунтовому луку с ходом тетивы 28 дюймов, мериканьские охотники с луком замеряли скорость с разной массой стрел


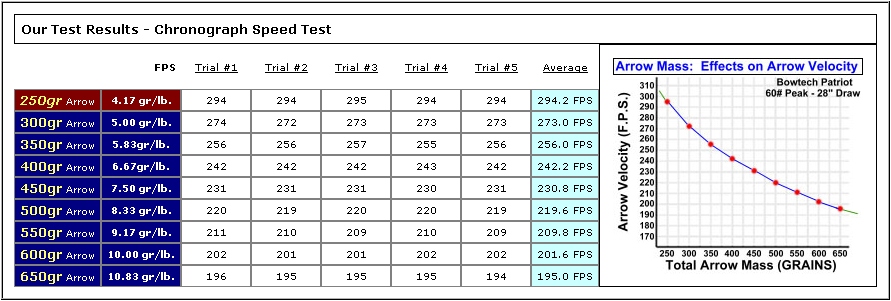
Похоже стройная теория была изначально ущербна, хотя.... Использовавшийся мериканами лук блочный, там другая силовая характеристика.
Но в целом картина верна - на легкой стреле скорость выше, но энергия ниже.
Если где-то ошибся - пинайте и поправляйте сразу. Дискуссия (конструктивная) приветствуется.
Лучники-практики, ваше мнение особенно интересно.

Слегка изменено

запись создана: 06.01.2012 в 14:51

@темы: Оружие, Луки-арбалеты

Comments

[Гость]

[Morceleb]

Гость, Есть что сказать, скажи.

[ЗЛОБНЫЙЗМЕЙ]

Не парься, если есть что сказать - говорят сразу. А этот гуглить ушел. Придет в звании К.О.

[Morceleb]

И то хлеб

[Morceleb]

Дискуссионное
с расчета начальной скорости стрелы?
Хорошо. Есть максимальная сила натяжения лука, которую может обеспечить человек, исходя из его анатомии и физиологии.
Далее есть лук, который растягивается на длину так же ограниченную анатомией.
Есть энергия, которую лук может запасти и передать стреле.
E=((Fm+F1)/2)*L*КПД, где Fm - максимальное усилие натяжения тетивы, F1 - усилие натяжения тетивы в начальной точке.
КПД лука в зависимости от конструкции и используемых материалов - от 20 до 60-65 (на блочных луках из композитных материалов) процентов.
Далее, в зависимости от веса стрелы лук успевает во время выстрела передать стреле часть запасенной энергии - вот здесь уже до 75-80%. Здесь важно подобрать стрелу по весу для того, чтобы получить КПД повыше, причем у тяжелых стрел этот показатель несколько выше, чем у легких. То есть возникает своего рода парадокс - энергия у тяжелой стрелы будет выше, но скорость ниже, тут уж выбирай что нужно.
Но для сверхдальней стрельбы неплохо бы иметь легкую стрелу с высокой начальной скоростью и хорошей аэродинамикой. Тут появляется забавный момент - теоретически, лучшей аэродинамикой обладает стрела без оперения, но она летит неточно и вибрации в ней гаснут несколько медленнее, чем в оперенной стреле, что опять же ведет к некоторому увеличению ее сопротивления полету.
Здесь снова появляется парадокс - легкая стрела будет иметь маленькую поперечную нагрузку и вследствие этого терять скорость быстрее, чем тяжелая стрела.
При этом увеличение силы натяжения лука требует усиления стрелы, а значит и увеличения ее веса. Следовательно снижения начальной скорости.
В результате мы имеем предел по силе натяжения, обусловленный физиологией человека (те самые человеческие возможности), предел по КПД собственно лука, обусловленный необходимостью разгонять не только стрелу, но и плечи лука и тетиву, а так же упругостью материала, из которого лук изготовлен, предел по передаче энергии стреле и, как это ни прискорбно, предел максимальной скорости стрелы, вытекающий из предыдущих пределов.
Фактически, предел скорости стрелы из лука - это чуть более 120 м/с для блочных луков.
Дальше в дело вступают аэродинамика и баллистика,
Вот здесь действительно плотность атмосферы и гравитация сыграют немалую роль.


Я бы дал пояснения, почему и в Арде невозможно получить существенного преимущества в дальности стрельбы из лука относительно других луков аналогичной конструкции А вот дали бы...
Хорошо. Увеличиваем усилие натяжения лука с 40 до 60 кг при начальных 10 и 15 соответственно.
Считаем энергию, запасаемую луками. КПД принимаем равным 30%, натяжение тетивы 60 см.
E=((Fm+F1)/2)*L*КПД=(400+100)/2*0.6*0.3=45 дж
E=((Fm+F1)/2)*L*КПД=(600+150)/2*0.6*0.3=67,5 дж.
Казалось бы, потенциальная энергия в полтора раза выше.
Здорово.
Стрелу тоже берем одинаковую, оптимизированную для более слабого лука (слабых лучников больше, чем могутных, как ты ни крути).
Для оптимизированной стрелы энергия будет примерно 80% потенциальной, для более легкой - меньше. Скажем, 70%.
Итак, в результате:
Естр1=36 дж
Е стр2=47.25 дж.
При весе стрелы в 30 г скорость соответственно 49 и 56 м/с. Это при увеличении силы натяжения в полтора раза.
Допустим, что стреляем мы в безводушном пространстве.
В этом случае дальность выстрела составит 244 и 319 м соответственно, то есть при увеличении силы натяжения в 1.5 раза дальность стрельбы растет всего на 30% в идеале. Но, увы, высокоскоростная стрела теряет скорость быстрее, чем низкоскоростная (сопротивление трения нелинейно), поэтому прирост дальности будет не столь значительным.
Таким образом, в любом мире, за исключением безвоздушного, прирост дальности будет не так уж и значителен.
Я ответил на Ваш вопрос?

[Гость]

Для определения потенциальной энергии лука можно использовать формулу: E=((Fm+F1)/2)*L*КПД

Формула с ошибкой, надо вычитать т.е. E=((Fm-F1)/2)*L*КПД иначе энергия лука завышена.
L - ход тетивы.

Прикидываем потенциальную энергию для лонгбоу с максимальным усилием натяжения 70 фунтов. На начальном участке сила натяжения не превышает 10 фунтов

70 -10 = 60 фунтов или 266Н (1 фунт - 0.4536кг или 4.45Н)
L пусть будет 0.5м
КПД ~ 50%
E = 266*0.5*0.5/2 = 33Дж а не 110Дж, это у мощных арбалетов такая энергия может быть...

[Morceleb]

Гость, Стоп, в конце прохождения тетивы на стрелу все равно воздействует (теоретически да, если стрела на этом участке уже не обгоняет тетиву) тетива, если же лук рекурсивный, то даже в начале натяжения уже нужно прилагать усилие, чтобы сдвинуть тетиву.
Поэтому с утверждением о вычитании силы натяжения в конце прохождения тетивы я категорически не согласен.

[Гость]

Поэтому с утверждением о вычитании силы натяжения в конце прохождения тетивы я категорически не согласен.

Энергия любой сжатой пружины
U = k(L1-L2)^2/2
Не важно что пружина была была предварительно напряжена, точно также и с потенциальной энергией, важна разность, суммирование неверный подход.

[Гость]

Извините за вмешательство в вашу дискуссию,но на мой взгляд,оба вы не правы. Формула для потенциальной энергии тетивы лука должна быть такой : Е=((Fm-F1)/2+ F1)xLxКПД. Сюда я попал случайно,гуглил. Так как на другом сайте хочу поставить одного товарища с небес на землю. Он возомнил себя большим ученым,якобы разрабатывающим новые теории об устройстве мира. При этом игнорирует всех предыдущих великих ученых,включая и Альберта Эйнштейна. А по мне все его "научные" работы представляют собой банальные фельетоны. В данном случае он представил одно свойство стрельбы из арбалета как парадокс. А я с этим не согласен. Кстати,мне 66 лет.